撰稿：张槐（课程撰写组）　摄影：傅秋莲　　组稿编辑：李泓

　　马克吐温曾说谎言有三种：谎言、混账谎言和统计。还有人说，把所有的局长都放到沙漠中去只有统计局的局长不怕旱，因为他水分最多。但统计又广泛的应用于社会科学、人文科学、物理、医学、心理学、及运动科学等各个领域。尤其在今日，由于数据收集的方便，加上计算机和统计软件的快速发展，更使得各行各业均纷纷使用统计方法来帮忙做决策。比如：公司里生产部门的管理人员常用统计方法来协助做好质量控制；经济学家常用统计方法来预测未来经济的发展趋势等等。以至于我们面临一种尴尬，我们不太相信统计数据，我们由不得不使用统计数据，恨他又离不开他。统计中有何玄妙，我们又该如何让统计来为你的决策服务？下文带你进入李庆琦教授的课堂来一探究竟。

李庆琦教授

什么是统计
　　统计，英文称为Statistics，是一门牵涉到数据的收集、整理、描述和分析的科学。做为一种科学研究的方法与工具，统计的主要应用在于利用相对小的样本来推测未知的总体，即以部分样本的特征来推断整体的特征，所以，正确的使用统计方法可以帮我们节省许多时间和金钱，并得出基本上还不错的结论。

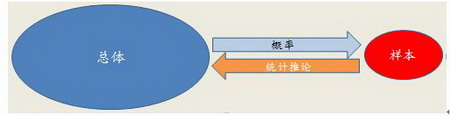
　　但是统计中的推论不是数学的证明。数学证明是具有确定性和可传递性的，当A可推出B，B又可以推出C时，必然有A可以推出C，（A→B，B→C；则A→C）；统计永远具有不确定性，统计描述的是一个事物发生或不发生的概率，是一种可能性，所以它具有不准确的风险，但它也并非是算命先生乱猜。比如说天气预报：算命先生告诉你的是晴时多云偶阵雨，那么统计能告诉你今天有80%可能性会下雨。
因为统计有不确定性，所以懂得统计变得更加重要，就算工作上不需要用到统计的人也是如此，因为统计也会撒谎，统计数字往往可以误导人。拥有基本的统计知识可以帮助我们更为正确地解读统计数据。同时，也较不易为坊间随处可见的统计所困惑。

如何选好基金
　　假如我们现在有10只（A-J）基金可够选择，并且知道他们过去10个月里每个月的收益率，我们该怎样从中去选择优质的基金来进行投资呢？具体每月收益率数据如下表所示。当看到这样一大版数据时，我们第一反应就是比较乱，也许我们各有各的方法来选择基金，但你敢肯定的说你的方法是最科学的么？下面看看学了统计的人会怎么做。

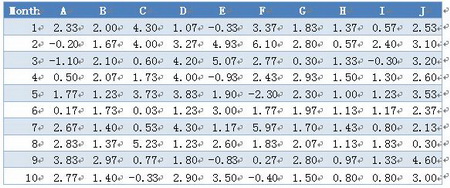
　　统计中有很多用数值来描述整体数据的特征，如平均值、众数、中位数、方差、标准差、比率等。其中方差和标准差尤为重要，计算如下，我们将看看标准差如何来帮助我们进行基金选择。

方差：  

 标准差：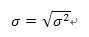 

其中μ是总体样本的平均值，n为样本数量

　　方差衡量的是，一组数据中，所有点到平均值的「平均平方距离」。而标准差则是方差的平方根。这个数值没有一个简单的直观解释，但可以约略的解释为，一组数据中，所有点到平均值的「平均距离」。
在财管及投资决策里，方差或标准差常被用于评估投资风险。方差或标准差愈大代表风险愈大，反之则风险愈小。一般而言，大部份投资者都希望选择平均回报高而风险又小的投资方案（如股票、基金、定期存款等），即我们要选择平均收益率高但标准差较小的基金。
　　每个基金收益率的平均值及标准差计算如下。

　　为了方便比较，我们将这些平均值及标准差做成一个散点图，每个散点代表一个基金回报率的平均值及标准差。值得特别注意的是，我们刻意将纵坐标的数值倒着画以便比较。

 
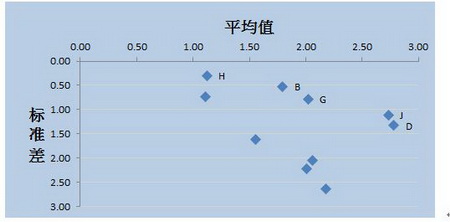
　　虽然我们无法从图上看出那个基金最好，但根据平均值愈大愈好，标准差愈小愈好的原则，我们却很容易看出那个基金不好。以任一代表某基金的散点为标准，任何位于其左下方的基金均不如它；而反过来说，任何位于其右上方的点均比它好。
　　根据上述的原则将不好的基金淘汰掉，剩下的就只有H、B、G、J、D等5个基金。事实上，我们也可用B和J的投资组合将G淘汰。由此我们可以得出H、B、J、D等4个基金，再根据我们的风险偏好来自行选择，这比我们面对一团乱糟糟的数据而无从下手要明了许多，我们做出的决策也变得科学很多，由此我们可以看到统计的在决策时的作用和魅力。

怎样做出更靠谱的估计
　　生活和工作中我们需要不断的做出各种估计，但我们的估计结果是根据什么做出来的呢？往往是一些历史经验或专业知识。那么下面就有一个问题：
　　某个国家成年男性的身高平均为170公分，标准差为 7公分。试估计该国有多少百分比的成年男性身高超过180公分？
　　这是一个十分庞大的问题，虽然我们有历史经验数据，但要我们做出一个比较准确的估计显然是很困难的，但如果我们学习了统计知识，引入统计学中的正态分布那么问题就变得简单了很多。
　　正态分布（Normal Distribution）是统计学里最重要的观念之一。如下图所示，一个呈正态分布的模型总体具有下列特征：总体中的数值分布密度最高的地方（曲线的最高点）位于分布的正中央，而该中心点正好也是总体的平均值、中位数、和众数之所在（三者的值相等）。以分布的中心点为基准，分布的左右两边呈完美的镜面对称。

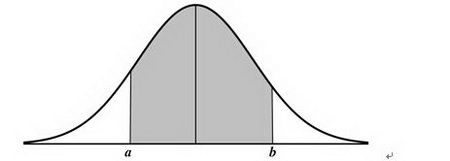
　　正态分布是一个「连续型分布」，用以描述一个连续型随机变量所有可能取值的分布情况。正态分布的钟形曲线乃由以下的「正态分布概率密度函数」定义而出：

 
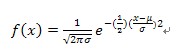
　　其中e = 指数常数 = 2.71828… p = 圆周率 = 3.14159… m = 分布的「平均值」 s = 分布的「标准差」
　　要计算一个从正态分布中随机抽取的数会介于a与b两个值之间的概率（或者说，分布中有多少百分比的数值是介于a与b之间），我们必须计算「在钟形曲线下介于a与b两点之间的面积」，也就是上图所示阴影部份的面积。在现实生活中，很多事物的分布都接近于正态分布，人的身高与体重、标准考试成绩的分布（如CPA、CFA、GRE等）、选民投票的选择、二次项式的分布、以及统计样本均值的分布等等。
　　由上面的讨论我们可以知道该国的男性身高该近似于正态分布，那么我们就能利用正态分布的特点来对身高超过180公分的男性百分比进行估计。
　　180公分比平均值（170公分）高出1.43个标准差。查阅正态分布表可知，在正态分布中随机选取一个数，其值会介于平均值(170)及另一个比平均值高出1.43个标准差的值(180)的概率是0.4236。所以，成年男性身高超过180公分的百分比为0.5 – 0.4236 = 0.0764，即7.64%。
　　如估计男性的身高一般，我们可以在生活和工作中灵活的运用正态分布来估计或预测很多事情，当事物近似于正态分布时，便能由样本的平均水平来估计总体的平均水平，从而对总体有一个跟准确的认识。比如，根据部分随机选择测试的工人生产效率，来估计整个工厂工人的生产效率，并以此来估计一段时间工厂产量，这有助于生产决策。

究竟是谁引起的成本
　　假如一个公司想了解自己公司的运输成本，分析运输费与重量和运输距离的关系，勿须置疑，距离和重量都是影响运输费用的因素，但他们究竟是怎样影响费用的变化呢？
　　某研究员随机抽样了20件包裹的数据。大体如下表所示：（篇幅原因只列示10件具体数据）

　　虽然我们能抽样得到20件包裹的成本费用信息，可以知道距离越远、重量越重则运输费用越高，但我们还是很难说清楚运输费用与重量和距离的具体关系。如何得到他们之间准确的关系呢？当我们说不清楚时，统计又一次能帮助我们了。
　　回归分析是一种统计方法，用以分析一个随机变量Y和一个或多个非随机变量X之间的关系，并找出最适合描述该关系的数学方程式。其中称Y为因变量或依赖变量，X为自变量或独立变量。在回归分析中，我们假设因变量和自变量之间有着如下列数学式所示的线性关系：

　§  Y = b­₀ + b₁X₁ + b₂X₂ + K + b_kX_k + e

　　其中e是随机误差。
　　我们可以对上面问题中的运输费用、重量和距离建构如下的一个回归模型：

§ E(y) = b₀ + b₁x₁ +b₂x₂，

　　y = 运输费（元） x1 = 包裹的重量（磅） x2 = 运输距离（英里）
　　将以上表中抽样得到的数据利用EXCEL或其他回归软件进行回归分析得到一个回归模型。

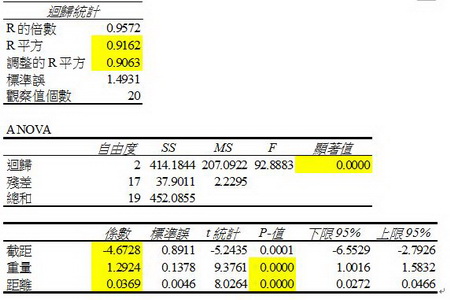
　　但得出的回归模型可能没多大意义，除非它能在下列三种衡量指标上得到令人满意的结果：
　　R2 ：是评估回归线与数据拟合程度的重要指标，R2 的值永远介于0和1之间。R2越高，模型与数据的拟合程度就越好。
　　总体F检验：用来检定一个回归模型，总体而言，是否一个有用的模型。F检验中：假设H0 是Y与自变量X没有线性关系。若H0为真，F值便不太可能很大。报表中愿望p值告诉我们，若H0为真时，会得到该F值的概率。若p值很小，则H0为真的可能性就不大。
　　个别t检验：用来检定因变量Y与每一个自变量Xi 之间的关系是否显着。个别t检验中：依然假设H0 是Y与自变量X没有线性关系。若H0为真，ｔ的絶对值便不太可能很大。报表中p值告诉我们，若H0为真时，会得到该t值的概率。若p值很小，则H0为真的可能性就不大。
　　在本例中，注意回归模型中标黄部分，R2=0.9162值比较大，，代表模型和数据的拟合程度相当不错；总体F检验的F值为92.8883，相对p-值几乎为0。所以总体而言，这个回归模型是有用的。个别t检验的结果显示，「重量」和「距离」两个变量的p-值都非常小（几乎为0），表示「费用」与「重量」和「距离」均呈显着的「正相关」。
故由回归模型的系数可得出回归方程式： 

　　 费用 = -4.67 + 1.29 重量 + 0.0369 距离

　　由回归方程可知运输费用的构成：重量每增加一磅，运输费用平均增加$1.29。距离每增加一英里，运输费用平均增加 $0.0369。而且我们还可以此来预测不同重量和距离的运输费用，比如5磅物品运输100英里的费用 = -4.67 + 1.29(5) + 0.0369(100) = 5.47。由以上运输成本线性关系我们可以推广到日常工作，比如运用回归模型分析资源投入对产出的影响，财务状况指标对股价的影响，成本因素分析等等。

　　从上文来看，统计存在我们生活和工作中的方方面面，当我们科学的运用统计分析方法来分析事物时，有助于我们更高效接近总体本质特征，理顺不同变量之间的关系，从而做出更符合实际规律的决策。当然我们不能说正确运用统计学后做出的决策就是一定正确的，但我们能保障这是一个基本还不错的决策，更加接近于科学。统计学的知识博大精深，上文只是列举了统计学中几个基本概念，海量的真知待作为读者您来自我学习与发现，本文也只能呈现出李庆琦教授丰富幽默的课堂内容的冰山一角。

EMPAcc　
　　2002年，学院与香港中文大学工商管理学院合作推出了高级财会人员专业会计硕士项目（EMPAcc），致力于培养“具有国际一流水准的中国CFO”。该项目是我院最早举办的学位项目，也是国内第一个专业会计硕士学位项目。
　　项目课程强调理论与实务并重，重点培养学员将国际最新的经济、财务和会计理念和方法运用到实践中的能力。成绩合格颁发香港中文大学高级财会人员专业会计学硕士学位及上海国家会计学院财务总监资格培训证书。项目70%的师资是香港中文大学的资深教授，他们都在北美取得博士学位，拥有多年的企业咨询经验和职业经理人培训的教学经验。其余的师资由上海国家会计学院本院师资或聘请境内外商学院的知名教授以及大陆政府界和实务界的精英担任。

（编辑：李泓）